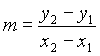Here are some notes about using MS Word 97 to type many of the mathematical symbols that may be needed for future labs.

If you are going to type an equation in the middle of a paragraph, be sure that you respect the order of operations. It may be necessary to use more parentheses than you are used to. For example, the slope of a line through two points (x₁, y₁) and (x₂, y₂) is given by m = (y₂ - y₁) / (x₂ - x₁). Notice that this says that you subtract y₁ from y₂, subtract x₁ from x₂, and then divide the result. This is correct.

However, if you write that the slope of the line is m = y₂ - y₁/x₂ - x₁, then you are technically incorrect. This says that first you divide y₁ by x₂, subtract the result from y₂, and then subtract x₁ from that result.

The standard keystrokes for the elementary operators are:

+ addition
- subtraction
* multiplication
/ division
= equality
< less than
> greater than
( ) parentheses
[ ] square brackets
{ } braces
! factorial
% percentage
^ exponent
| or : such that in set notation

You can use these in when you are typing normal text. I assume that you are all familiar with the set of real numbers. This is usually denoted with a bold face R. (You might have seen the symbol Â. To type  , select Symbol from the Insert menu, highlight this symbol and click OK.) R has the property that the sum of two real numbers, a+b, is again a real number. As well, the difference, a-b, the product, a*b, and the quotient, a/b (for b non-zero), of two real numbers is again a real number. R also has the property that if a+b < a+c for real numbers a, b, c, then b<c. If x is a positive real number and a<b for any two real numbers a, b, then xa < xb. R is an example of what is called a field.

The set of all real numbers strictly between 0 and 1 is given by the set {x | 0<x<1}. You may have seen this written as {x : 0<x<1}. Both are equivalent.

The factorial operator is defined as follows. If n is a positive integer, then n! = n*(n-1)*(n-2)*...*3*2*1. For example, 5!=5*4*3*2*1=120.

An exponential function is any function, f(x), of the form f(x)=c*a^x, where c and a are constants and x is a variable.

You might prefer to use superscripts for the exponents. Then, an exponential function is any function, f(x), of the form f(x) = c*a^x, where c and a are constants and x is a variable.

To type superscripts (or subscripts, for that matter) select Font from the Format menu and choose the effect Superscript (or Subscript). Be sure to turn it off after you have finished superscripting (or subscripting).

The advantage of using MS Word 97 is that your mathematical formulas can be more complex because of the built in Equation Editor.

To use the equation editor, select Object from the Insert menu. Scroll down and double-click Microsoft Equation 3.0. This calls up a dialogue box which provides access to many mathematical symbols.

You might prefer to set some equation apart from the body of the main paragraph. For example, the slope of a line through two points (x₁, y₁) and (x₂, y₂) is given by

.

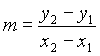Now immediately you will notice that there is an inconsistency in the style of the font used. That is, the variables used by the equation editor are italicized, while the variables that I have been typing up until now are not. I could remedy this by italicizing all variables in the previous paragraphs. Instead I will say that you should try to at least be consistent within a sentence. Thus, I would write the last sentence as:

?two points (x₁, y₁) and (x₂, y₂) is given by

.

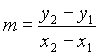I can now rewrite the definition of an exponential function in a form that may be easier to read. An exponential function is any function, f (x), of the form

where c and a are constants and x is a variable.

Finally, a couple of notes to make both of our lives easier! Mathematics is much easier to read if the symbols are not all crowded together. Do not hesitate to be generous with spaces. Although a+b is easy enough to read, you might prefer a + b. For more complex expressions such as (x^3+y^3)/(x^2-y^2)=(x^2-xy+y^2)/(x-y), spaces definitely help.

Now isn't (x^3 + y^3) / (x^2 - y^2) = (x^2 - xy + y^2) / (x - y) easier to read!

There are a couple of shortcuts that you can implement to make typing the paper faster. You can add shortcut buttons to your tool bar. To add a shortcut button for subscripting or superscripting, select Customize from the Tools menu, select the category Format and scroll down through the commands until you see the Subscript (or Superscript) button. Click on the button and drag it to the tool bar at the top of the screen. You can place the shortcut button anywhere you like on the tool bar. Now, whenever you want a subscript all you need to do is click the subscript button when you want to begin subscripting and click it again when you want to end.

To add a shortcut for the Equation Editor, follow the same steps. In the category Insert you find Equation Editor near the end of the list of commands. The button for the Equation Editor looks like the square root of the Greek letter alpha: